<X>(t) and its Fluctuations for Coherent and Squeezed States
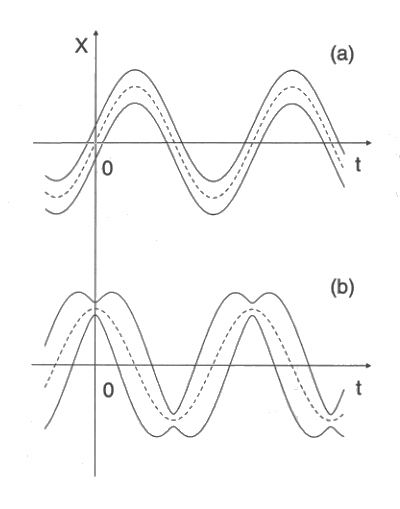
Schematic diagram of the time evolution of the expectation value <X>, and the fluctuation (<(DX)^2>)^0.5 of the dimensionless quadrature X (of an electric field, for instance) in a coherent state (a) and a squeezed state (b). Here dashed lines represent <X>, while solid lines represent the envelopes <X> ± (<(DX)^2>)^0.5, which are the upper and lower bounds of the fluctuating quantity X.
(a) A single-mode photon
coherent state |a>, where <X>
= 2R[e(aexp(-iwt))]
= 2|a|sinwt,
which means that a is purely imaginary; and
<(DX)^2> = 2.
(b) A single-mode photon squeezed state |aexp(-iwt), x(t)>, where the squeezing factor x(t) satisfies x(t) = rexp(-2iwt). Here, <X> = w|a|coswt, which means that a is real, and its fluctuation is
<(DX)^2> = 2[(exp(-2r)cos^2wt + exp(2r)sin^2wt)].
Notice that the squeezing effect appreas at the times when <X> reaches its maxima.
Image Source: X. Hu, Quantum Fluctuations In Condensed Matter Systems, UM Ph.D. Thesis 1997, Page 6.