Reversible Rectifier that Controls the Motion of Magnetic Flux Quanta in Superconductors
Science 302, 1188 (Nov. 14, 2003).
See also perspectives in Science 302, 1159 by H. Hilgenkamp, V. V. Moshchalkov, P. Kes; and Highlight: Science 302, 1111.
J.E. Villegas (1), Sergey Savel~Rev (2), Franco Nori (2,3), E.M. Gonzalez (1), J.V. Anguita (4), R. García (4), J.L. Vicent(1)
1 Departamento de Física de Materiales,
Facultad Ciencias Físicas, Universidad Complutense, Madrid,
Spain.
2 Frontier Research System, The Institute
of Physical and Chemical Research (RIKEN), Wako-shi, Saitama,
Japan.
3 Center for Theoretical Physics, Department
of Physics, University of Michigan, Ann Arbor, MI, USA.
4 Instituto de Microelectrónica
de Madrid, Centro Nacional Mícroelectrónica, Consejo Superior
de Investigaciones Científicas, Madrid, Spain.
Abstract
This paper describes a device
that controls the motion of flux quanta in a Niobium superconducting film
grown on an array of nanoscale triangular pinning potentials. The controllable
rectification of the vortex motion is due to the asymmetry of the fabricated
magnetic pinning centers. The reversal in the direction of the vortex flow
is explained by the interaction between the vortices trapped on the magnetic
nanostructures and the interstitial vortices. The applied magnetic field
and input current strength can tune both the polarity and magnitude of
the rectified vortex flow. Our ratchet system is explained and modeled
theoretically considering the interactions between particles.
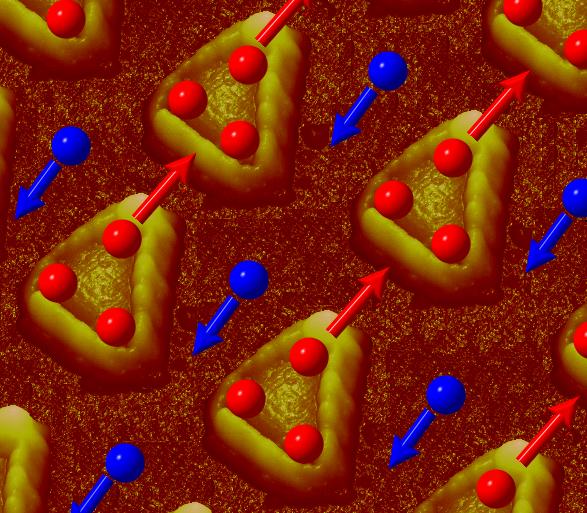
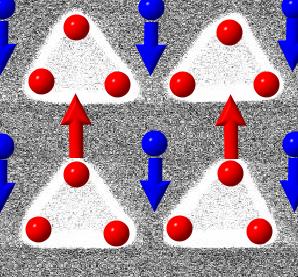
Schematics of vortex motion in nano-magnetic triangles.
Introduction
Motor proteins play a key role in the transport of materials at the cellular level. These biological motors are anisotropic devices that, driven by non-equilibrium fluctuations, bias the motion of particles, and are inspiring a new generation of solid-state devices that open new avenues for controlling the motion of, for example, electrons, colloidal particles, and magnetic flux quanta. We consider superconducting devices with anisotropic pinning, where the dc transport of magnetic flux quanta may be driven by an ac or unbiased current. The control of the motion of vortices using asymmetric pinning can be useful for applications in superconductivity, including field-dependent reversible vortex diodes and the removal of unwanted trapped flux in devices. Several different ways of using asymmetric pinning in superconductors to control vortex motion have been recently proposed. However experiments in this area have been difficult to control.
Earlier work on vortex dynamics in superconducting films with regular arrays of defects, using either non-magnetic or magnetic pinning traps, have explored a plethora of interesting physical effects, including matching effects with ordered submicron magnetic defects, interstitial vortices, random versus periodic pinning, and channeling effects in the vortex lattice motion. Now that the field of vortex dynamics on periodic pinning potentials is sufficiently understood, we are in the position to take the next step of manipulating and controlling the motion of magnetic flux quanta. Preliminary numerical studies of vortex dynamics on arrays of triangular pinning potentials have found that rectified vortex motion should occur, when the system is ac-driven.
Magneto-transport R(H) experiments were done with a magnetic
field H applied perpendicular to the substrate in a liquid Helium system.
Fig. 1B shows the R(H) data taken from the sample with the magnetic array
shown in Fig. 1A. The dc magneto-resistance exhibits commensurability effects
in which dissipation minima develop as a consequence of the geometrical
matching between the vortex-lattice and the underlying periodic structure.
At these matching fields, the vortex-lattice motion slows down, and R(H)
minima appear at equally spaced values of H: Hmatch(n)=nH1,
with H1=32 Oe being the first matching field, and
n the number of vortices per unit cell. Sharp minima in R(H) can be observed
at the 1st, 2nd and 3rd matching fields, but shallow and not well-defined
minima for higher matching fields. The difference between the sharp and
shallow minima in R(H) arises because by increasing the applied magnetic
field H beyond 3H1, interstitial vortices appear.
Thus, the maximum number of vortices in each triangle is three. Therefore,
for each matching field we know the number of vortices per unit cell, both
inside the traps and in-between them.
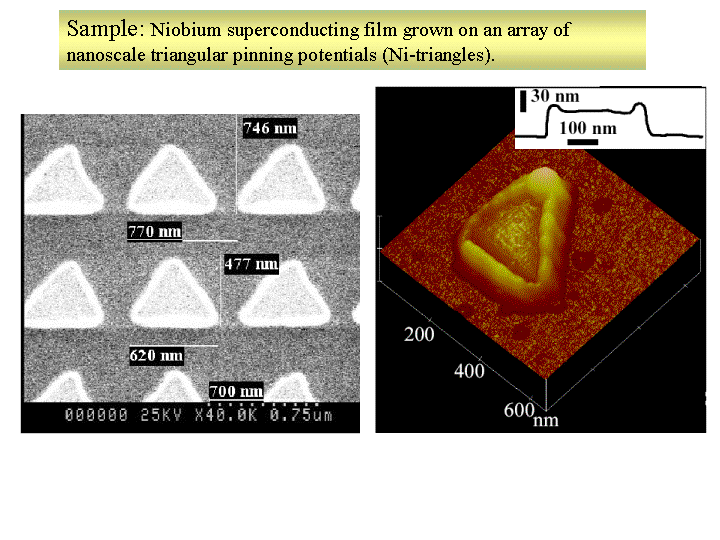Fig.1A
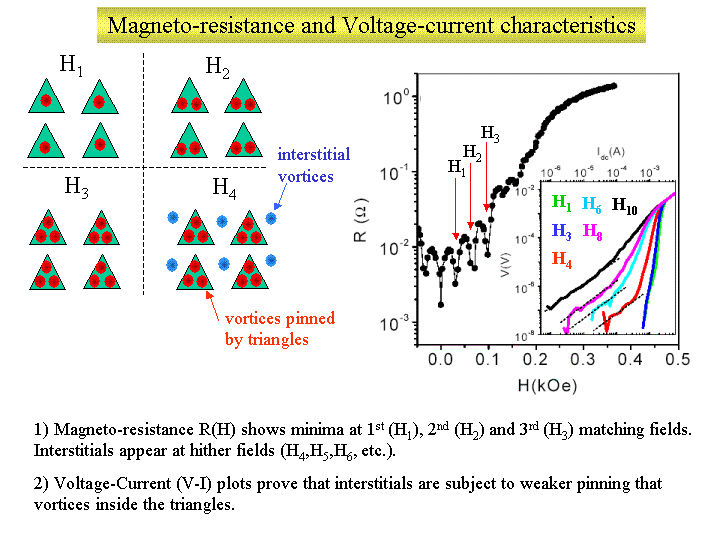Fig.1B
As shown in the lower inset to Fig. 1B, when increasing an applied dc current Idc, the interstitial vortices depin first, producing a linear increase, in a log-log plot, of the voltage versus current. With further increase of the applied dc current, the vortices that were initially trapped in the magnetic triangles begin to depin producing a faster increase in V(Idc). This illustrates that there are two types of vortices subject to very different pinning energies, their motion depending on Idc and the applied magnetic field.
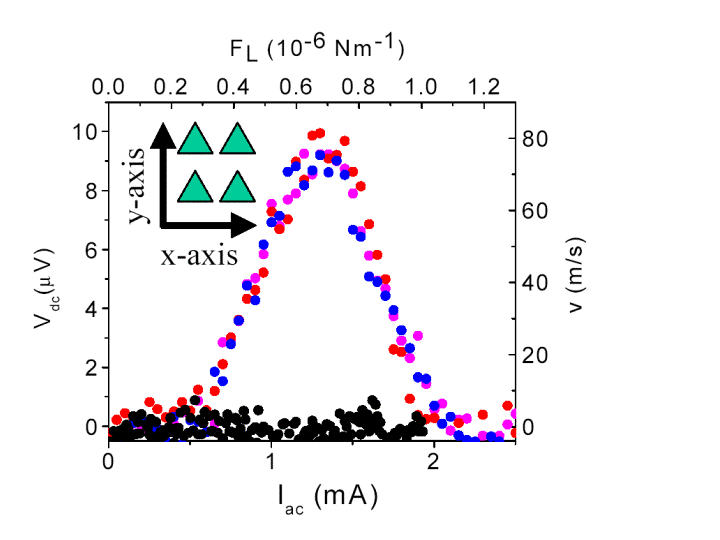Fig.2
Fig. 2 shows what happens when, at constant temperature and applied magnetic field H=H1=32 Oe, an ac current density J=Jacsin(wt) is injected along the x-axis. This yields an ac Lorentz force on the vortices along the y-axis. Although the time-averaged force on the vortices is zero, a non-zero dc voltage drop is observed (colored dots). As the electric field ( and being the vortex-lattice velocity and the applied magnetic field, respectively), the voltage drop along the direction of the injected current probes the vortex motion along the y-axis. We measure the voltage drop Vdc using a dc nanovoltmeter, and obtain the time-averaged vortex velocity. Thus, the vortex lattice moves on this asymmetric potential with a net velocity. To further test this behavior the ac current was injected along the y-axis (that is the vortex lattice was pushed along the x-axis) of the array. In this case the dc voltage was zero (black dots) because of the symmetric potential landscape along the x direction, resulting in a zero net velocity.
Fig.
3
At a constant applied magnetic field, the dc voltage increases when decreasing the temperature. At a constant temperature, increasing the applied magnetic field produces the effect shown in Fig. 3. Because we know the number of vortices in each unit cell of the array, the analysis of the experimental data is clearer for applied matching fields. The amplitude of the dc signal decreases when increasing the magnetic field because the effective pinning is suppressed by the inter-vortex repulsion. Moreover, when n>3 (corresponding to more than three vortices per unit cell), a dc reversed signal begins to develop with a maximum (shown by the blue arrows) occurring at a lower Lorentz force than the positive dc maxima (red arrows). The interstitial vortices, which feel a weak and inverted ratchet potential, move in the opposite direction than the vortices pinned at triangles, which are subject to a strong ratchet potential. This inverse-polarity current effect is enhanced when increasing the magnetic field (Fig. 3C–3D) and finally, at very high magnetic fields, close to the normal state, a complete dc voltage reversal occurs (Fig. 3F). The measurements are done near Tc in order to suppress the random pinning compared to the triangular pinning. For slightly lower values of T, pinning becomes stronger, requiring larger applied currents to depin the trapped vortices, but the same trend shown in Fig. 3 is also observed.
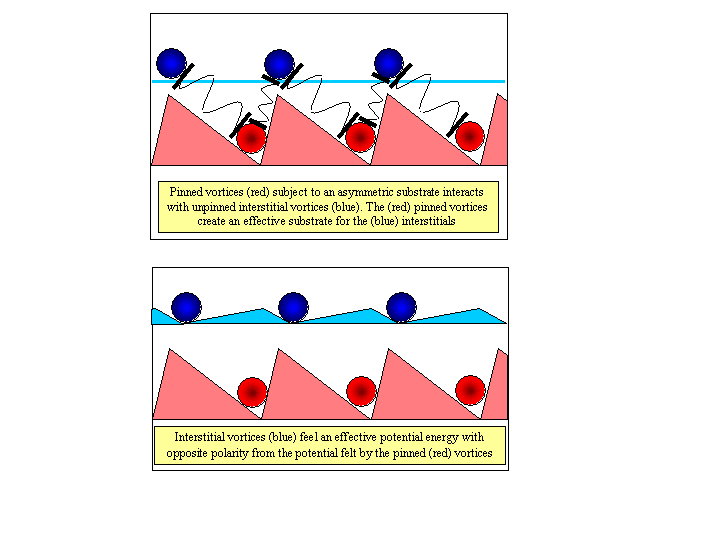Fig.
4a
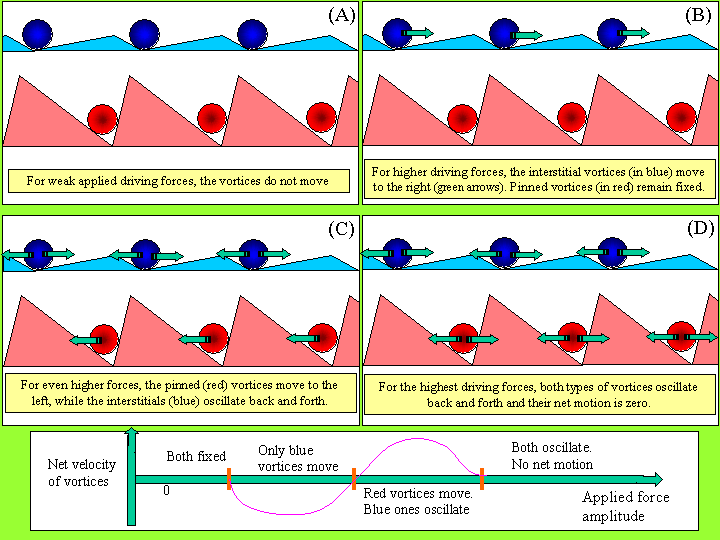Fig.4b
In order to interpret the experimental results, we can separate all vortices in two groups: (i) pinned vortices, which move from one triangular-shaped pinning trap to another one and, thus, these are directly affected by the pinning potential; and (ii) interstitial vortices, which move in-between triangles, and do not directly interact with the pinning traps. However, the interstitial vortices can indirectly feel the spatial asymmetry via their interactions with the pinned vortices.
This problem can be mapped into the similar system of two species of repulsive particles [S. Savel'ev, F. Marchesoni, F. Nori, Phys. Rev. Lett. 91, 010601 (2003)] in which one type or species of particles (pinned vortices for our experiments shown in red in Fig. 3G–3J) directly interacts with the spatially-asymmetric substrate. The other type of particle (interstitial vortices here, shown in blue in Fig. 3G–3J) is insensitive to the substrate, at least in a direct manner (Fig. 4a). It has been shown in that those particles (assigned red) subject to the substrate potential create an effective asymmetric potential, with the opposite asymmetry or opposite polarity, for the other (blue) particles (Fig. 4b) — if these two species repel one another. When all the particles are subjected to an ac drive force, this “inverted-polarity” potential rectifies the motion of the blue particles (interstitial vortices in our case) in one direction, and the original pinning potential rectifies the motion of the red particles (pinned vortices) along the opposite direction, because the latter feel a potential with opposite polarity (Fig. 4b).
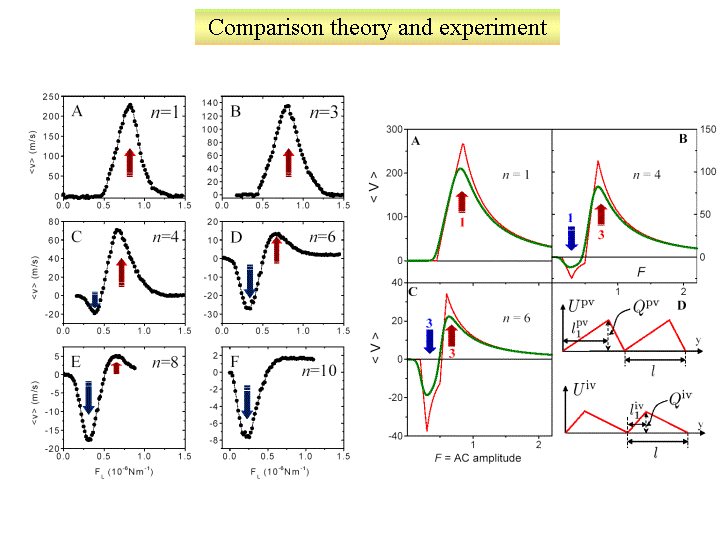Fig.
5
This simple model qualitatively describes the experimental data (Fig. 5).
Conclusions:
Our device allows a versatile control of the motion of vortices in superconducting films. Simple modifications and extensions of it would allow the pile up (magnetic “lensing”), shaping, or “sculpting” of micro-magnetic profiles inside superconductors. Thus, vortex lenses made of oppositely-oriented triangles would provide a strong local increase of the vortex density at its “focus” regions. Thus, extensions of these type of systems should open new avenues for motion control of flux quanta and provide a first step towards a new generation of devices based on the flow of magnetic flux quanta.